Polygonmodellierung
Polygon- oder Drahtgittermodelle basieren dabei auf Punkte (engl. points oder vertices) im dreidimensionalen Koordinatensystem (‚Raum‘ in der virtuellen Welt der 3D-Anwendung), die durch ‚Kanten‘ (engl. edges) miteinander verbunden werden, um eine Form zu erstellen. Drei auf diese Weise miteinander verbundene Punkte bilden dabei eine logische Fläche (engl. surface oder face) in Form eines Dreiecks (engl. triangle oder oft mit tri abgekürzt), die kleinstmögliche Art eines Polygons mit drei Ecken. Diese Flächen können aber auch vier, fünf, sechs, oder x weitere Ecken haben, weswegen man allgemein von Polygonen (Vielecken) spricht. Setzt man nun verschiedene solcher Flächen aneinander, kann man daraus ein dreidimensionales Objekt formen, das durch die Punkte und Kanten wie ein (Fischer-)Netz oder Drahtgitter aussieht, weswegen diese Modelle auch Drahtgittermodelle (engl. wireframe models) genannt werden.
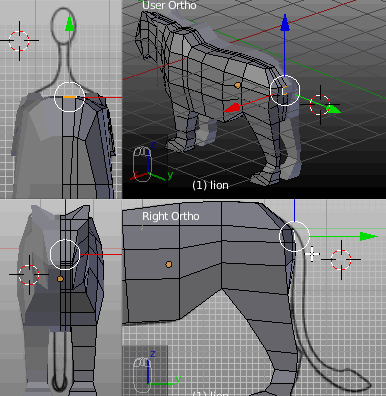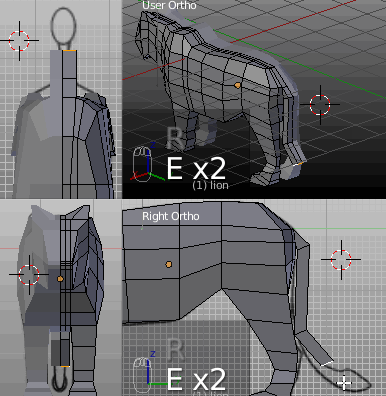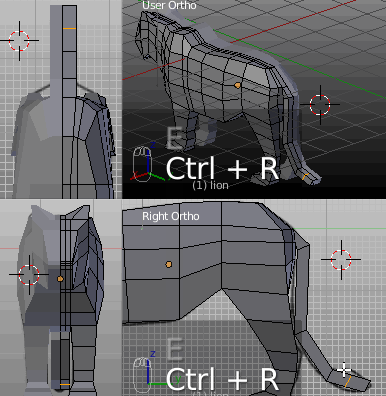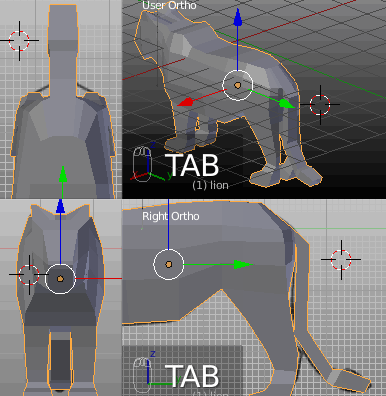
Solche Drahtgittermodelle können freihändig (z.B. anhand einer Zeichnung oder Fotographie als Vorlage, anhand derer die Form mit Punkten und Kanten nachgebaut wird) oder von simplen Standardformen wie Würfel, Zylinder, Kugel, usw. aus erstellt werden, von denen dann einzelne Flächen herausgestellt (engl. extruding) und in die gewünschte Form gebracht werden; meist läuft es auf eine Kombination beider Ansätze hinaus, die durch viele weitere Modellierungswerkzeuge verfeinert werden.
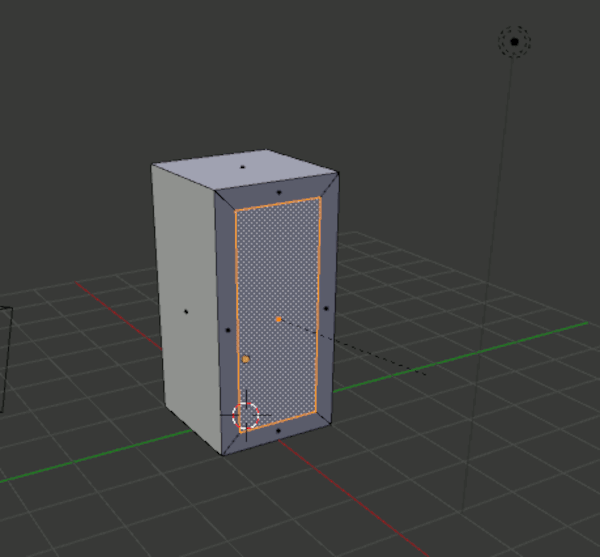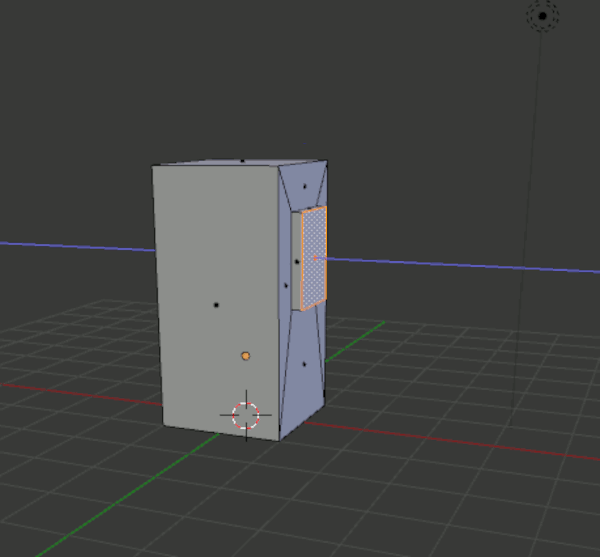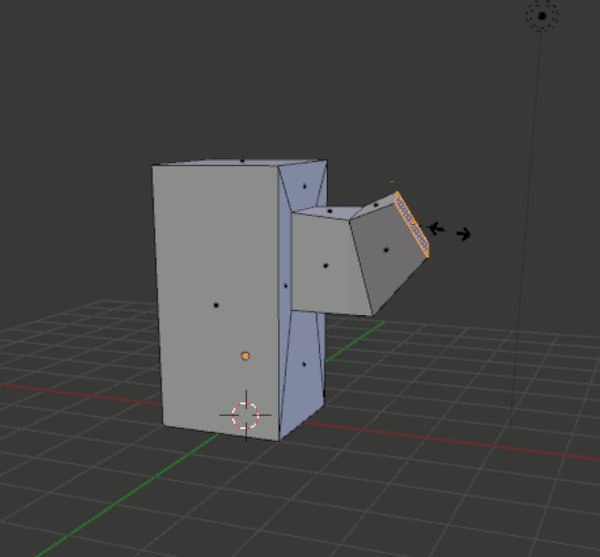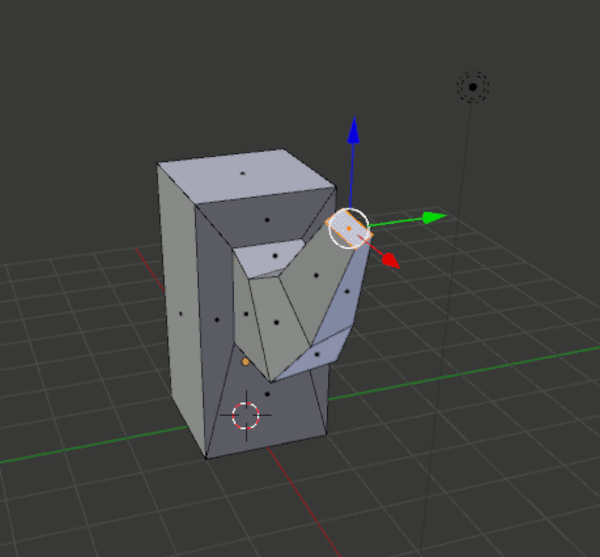
Standardform (engl. primitive), in diesem Fall ein Quader.
Herausstellen von Flächen (engl. extruding).
Freihändige Modellierung anhand einer zeichnerischen Vorlage.
Generell gilt hierbei: Je mehr Punkte und Polygone in dem Modell eingebaut werden, desto detaillierter ist das 3D Modell (vgl. dazu analog die Auflösung von Rastergrafiken); zoomt man jedoch stark in ein solches Modell hinein, erkennt man die einzelnen Komponenten, da auch genuin runde Oberflächen oder Objekte wie z.B. ein Zylinder oder eine Kugel aus diesen Vielecken bestehen, also aus aneinander gefügten Punkten und Kanten, die gerade sind und nur aus größerer Entfernung rund erscheinen.